理解贝叶斯理论 Understanding Bayes theorem
目前为止我看到理解贝叶斯公式最好的方式是通过绘图,来自3Blue1Brwon频道讲解贝叶斯的视频,详情可参阅上述视频(以下三幅图也来自该视频)。
最常见的一个误解来自于P(A and B) = P(A)P(B),事实上这个公式并不成立,左右两边并不一定相等;因为它有一个前提条件是A事件与B事件相互独立,我们常常看到在掷硬币、掷骰子之类的例子中,因为每次投掷相互独立、互不影响,因此计算概率时可以将每次的概率直接相乘,但实际生活远比这个复杂,因为两个事件可能有或多或少的关联,影响事件的因素有很多,此时贝叶斯就会熠熠生辉。
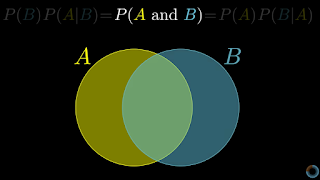 |
| P(A and B)≠ P(A)P(B) |
 |
| P(A and B)作为中介 |
 |
| 推导贝叶斯公式 |
ps:利用概率和贝叶斯思考方式对于生活很有指导意义,帮助我们借助于新信息更新已有认知。
生活中的现象:常常不自觉担心这个、担心那个,但细细思考一下,最简单的方式就是看一下这件事情发生的概率有多少?比如一个地区,每年因为下雨掉沟里的人有15人,该地区一共有10万人,那你计算一下如果今天下雨了,你担心的那个人掉沟里的概率是多少,是0.15%,就是说2000人里才有3个人因为这件下雨掉沟里,你还会像之前那样担心吗?
但现实生活的情况往往比较复杂,会有很多信息可以借鉴,此时就要用到贝叶斯思考方式。
什么是贝叶斯公式?
比如说小爱同学一直认为自己的男朋友天猫精灵是个很老实的人,但某一天当小爱同学不小心翻到了天猫精灵的互动记录,发现天猫精灵与多位异性有频繁互动,此刻的小爱同学是矛盾的,她想:天猫精灵出轨了吗?这个判断其实是不好确定的,小爱坐在沙发上,开始自言自语,突然有个苹果扔了过来,是贝叶斯的苹果,小爱很激动,突然想起贝叶斯老师曾经教授她的秘笈,小爱拿出一张纸开始推演起来:原本小爱认为小天是个老实人(不出轨)的概率是90%,也就是小爱认为小天出轨的概率是10%,而出轨情况下与多位异性互动的概率假设是70%,假设不出轨的话跟多位异性互动的概率是5%,那么根据贝叶斯公式,就可以计算出在发现小天与多位异性有频繁互动的前提下,小天出轨的概率:
P(出轨 | 频繁互动)= P(频繁互动 | 出轨)* P(出轨)/ P(频繁互动),而其中P(频繁互动)= P(频繁互动 | 出轨)*P(出轨)+P(频繁互动 | 不出轨)*P(不出轨),因此可以计算得到P(出轨 | 频繁互动)= (70%*10%)/ (70%*10% + 5%*90%)= 60.87%,可见此情此景下小天出轨的概率也就比随机的50%高了一点点,事实上当小爱进一步把小天的工作性质考虑进来之后(毕竟作为在公园工作的智能音箱,频繁互动不可避免),更加确信小天并没有出轨。这是一个极其简单的例子。
More needs to be updated.

评论
发表评论